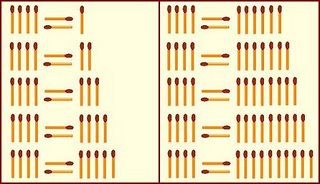
Esta vez les propongo un sencillo juego que, salvo alguna variación, debo haber visto por ahí, pero no recuerdo la fuente.

Se trata de reubicar los fósforos que hay en uno (y sólo en uno) de los lados de cada igualdad, de manera que ésta se cumpla, es decir: formar una expresión con numerales romanos (correctamente escritos), que puede ser un número o una operación aritmética, de modo que al resolverla dé la cantidad exacta de fósforos que hay al otro lado.

Para ello debes utilizar sólo las cuatro operaciones básicas que se forman con los fósforos (por supuesto que se priorizan multiplicaciones y divisiones).

No está permitido romper ni trasladar fósforos de un lado a otro del signo igual.
En todos los casos se debe respetar la cantidad de fósforos que hay a cada lado.
Siempre en el lado izquierdo hay 4 fósforos y en el lado derecho varían de 1 a 10, en este caso.

Si alguien se quedó corto y desea seguir más allá, pues adelante, no tiene más que dejar en los comentarios sus hallazgos, si hay interés veré de postear una tabla mencionando el autor de cada solución, de hecho tenía la malvada intención de continuar la serie hasta el 2006 :-)…

Para obtener el deca de premio debes enviar la solución completa de la tabla hasta el 10 y un método que permita resolver el problema 2006, es decir :

IIII = IIIIIII … III (con 2006 fósforos a la derecha).

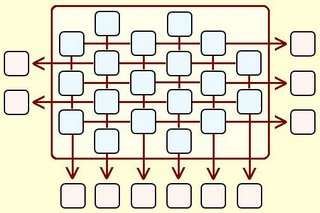
Coloca los números del 1 al 19 (sin repetir) y realiza todas las adiciones señaladas por las flechas. El objetivo es lograr que las sumas formen la mayor lista de números consecutivos posible.

En caso de haber sumas repetidas, éstas se consideran como un solo número cuando se conforma la lista.

En los comentarios iré dando a conocer los tamaños de las listas que vayan llegando.

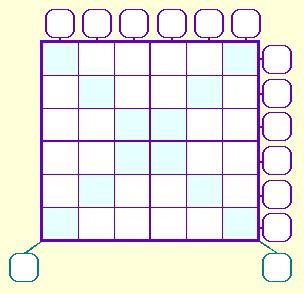El tablero de 6x6 casillas está dividido en 4 sectores de 3x3 casillas cada uno.
Debes colocar los dígitos del 1 al 9 (sin repetir) en cada uno de los sectores de tal forma que:

1) No haya dígitos repetidos en cada una de las filas, columnas o diagonales principales.
2) La suma de los dígitos de cada una de las dos diagonales principales debe ser la misma.
3) La suma de los dígitos de cada una de las filas y columnas del tablero debe ser diferente.

En esta ocasión voy a compartir con ustedes un hallazgo mientras intentaba crear un juego.
Tomé como base los primeros tres números naturales, los combiné para formar la siguiente adición:

¿qué tiene de extraordinario ésto?, muy sencillo, aparte de la igualdad numérica evidente (nótese que además utiliza los mismos dígitos), se me ocurrió escribirla así: